|
C趣味程序(二)(12)求4位以内的相亲数 |
|
|
|
www.nanhushi.com 佚名 不详 |
|
2.6 相亲数
2500年前数学大师毕哥达拉斯就发现,220与284两数之间存在着微妙的联系:
220的真因数之和为:1+2+4+5+10+11+20+22+44+55+110=284
284的真因数之和为:1+2+4+71+142=220
毕达哥拉斯把这样的数对A,B称为相亲数:A的真因数之和为B,而B的真因数之和为A。
相亲数的直接推广是相亲数链:呈连环套形式的多个相亲数。例如,A的真因数之和为B,B的真因数之和为C,C的真因数之和为D,最后D的真因数之和又为A,则A,B,C,D称为一个4环相亲数链。
数学界寻找相亲数与相亲数链,竟相打破最大相亲数记录的热情不减。
2.6.1 求4位以内的相亲数
1.算法分析
对指定区间中的每一个整数i应用试商实施穷举判别。根据相亲数的定义,用试商法(i mod j=0)找出i的所有小于i的真因数j,并求出真因数的和s。然后用同样的方法找出整数s的真因数之和s1。如果有s1=i,则i,s为相亲数对。
为减少试商j循环次数,注意到数i若为非平方数,它的大于1小于i的因数成对出现,一对中的较小因数要小于i的平方根。若数i愉为整数t的平方,此时t为i的一个因数,而不是一对,因而在和s中减去多加的因数t,这样试商j循环只要从2取到i的平方根t=SQR(i),可大减少j循环次数。缩减程序的运行时间。最后按规格打印所找出相亲数。
程序代码如下:
/*求4位以内的相亲数*/
#include<stdio.h>
#include<math.h>
void main()
{
int i,j,s,t,s1;
for(i=11;i<=9999;i++)
{
s=1;t=sqrt(i);
for(j=2;j<=t;j++) if(i%j==0) s=s+j+i/j;
if(i==t*t)s-=t; /*求i的真因数之和s*/
if(i<s) /*规定i<s,避免重复*/
{
s1=1;t=sqrt(s);
for(j=2;j<=t;j++) if(s%j==0) s1=s1+j+s/j;
if(s==t*t) s1-=t; /*求s的真因数之和s1*/
if(s1==i)
{
printf("相亲数:%d,%d\n",i,s);
printf("%d的真因数之和为:1",i); /*规格打印相亲数*/
for(j=2;j<=i/2;j++) if(i%j==0) printf("+%d",j);
printf("=%d\n",s);
printf("%d的真因数之和为:%d",s,1);
for(j=2;j<=s/2;j++) if(s%j==0) printf("+%d",j);
printf("=%d\n",i);
}
}
}
}
程序运行结果如下:
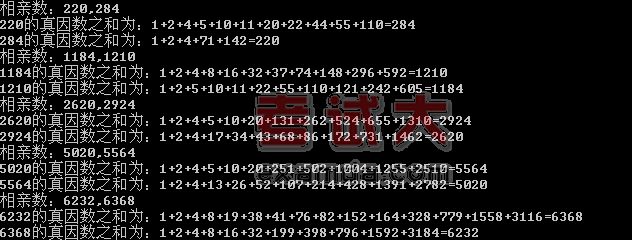
|
|
|
|
| 文章录入:杜斌 责任编辑:杜斌 |
|
上一篇文章: C趣味程序(二)(11)完全数
下一篇文章: C趣味程序(二)(12)求n环相亲数链 |
| 【字体:小 大】【发表评论】【加入收藏】【告诉好友】【打印此文】【关闭窗口】 |
| |
|

