 打印本文
打印本文  关闭窗口
关闭窗口 求四阶的素数幻方。即在一个4X4 的矩阵中,每一个格填 入一个数字,使每一行、每一列和两条对角线上的4 个数字所组成的四位数,均为可逆素数。
*问题分析与算法设计
有了前面的基础,本题应当说是不困难的。
最简单的算法是:采用穷举法,设定4X4矩阵中每一个元素的值后,判断每一行、每一列和两条对角线上的4个数字组成的四位数是否都是可逆素数,若是则求出了满足题意的一个解。
这种算法在原理是对的,也一定可以求出满足题意的全部解。但是,按照这一思路编出的程序效率很低,在微机上几个小时也不会运行结束。这一算法致命的缺陷是:要穷举和判断的情况过多。
充分利用题目中的“每一个四位数都是可逆素数”这一条件,可以放弃对矩阵中每个元素进行的穷举的算法,先求出全部的四位可逆素数(204个),以矩阵的行为单位,在四位可逆素数的范围内进行穷举,然后将穷举的四位整数分解为数字后,再进行列和对角线方向的条件判断,改进的算法与最初的算法相比,大大地减少了穷举的次数。
考虑矩阵的第一行和最后一行数字,它们分别是列方向四位数的第一个数字和最后一个数字,由于这些四位数也必须是可逆素数,所以矩阵的每一行和最后一行中的各个数字都不能为偶数或5。这样穷举矩阵的第一行和最后一行时,它们的取值范围是:所有位的数字均不是偶数或5的四位可逆数。由于符合这一条件的四位可逆素数很少,所以这一范围限制又一次减少了穷举的次数。
对算法的进一步研究会发现:当设定了第一和第二行的值后,就已经可以判断出当前的这种组合是否一定是错误的(尚不能肯定该组合一定是正确的)。若按列方向上的四个两位数与四位可逆数的前两位矛盾(不是其中的一种组合),则第一、二行的取值一定是错误的。同理在设定了前三行数据后,可以立刻判断出当前的这种组合是否一定是错误的,若判断出矛盾情况,则可以立刻设置新的一组数据。这样就可以避免将四个数据全部设定好以后再进行判断所造成的低效。
根据以上分析,可以用伪语言描述以上改进的算法:
开始
找出全部四位的可逆素数;
确定全部出现在第一和最后一行的四位可逆素数;
在指定范围 内穷举第一行
在指定范围内穷举第二行
若第一、第二、三行已出现矛盾,则继续穷举下一个数;
在指定范围内穷举第四行
判断列和对角方向是否符合题意
若符合题意,则输出矩阵;
否则继续穷举下一个数;
结束
在实际编程中,采用了很多程序设计技巧,假如设置若干辅助数组,其目的就是要最大限度的提高程序的执行效率,缩短运行时间。下面的程序运行效率是比较高的。
*程序与程序注释
#include<stdio.h>
#include<math.h>
int number[210][5]; /*存放可逆素数及素数分解后的各位数字*/
int select[110]; /*可以放在矩阵第一行和最后一行的素数的下标*/
int array[4][5]; /*4X4的矩阵,每行0号元素存可逆素数对应的数组下标*/
int count; /*可逆素数的数目*/
int selecount; /*可以放在矩阵第一行和最后一行的可逆素数的数目*/
int larray[2][200]; /*存放素数前二、三位数的临时数组所对应的数量计数器*/
int lcount[2];
int num(int number);
int ok(int number);
void process(int i);
void copy_num(int i);
int comp_num(int n);
int find1(int i);
int find2(void);
int find0(int num);
void p_array(void);
void main()
{
int i,k,flag,cc=0,i1,i4;
printf("there are magic squares with invertable primes as follw:\n");
for(i=1001;i<9999;i+=2) /*求满足条件的可逆素数*/
{
k=i/1000;
if(k%2!=0&&k!=5&&num(i)) /*若可逆素数的第一位不是偶数或5*/
{
number[count][0]=i; /*存入数组*/
process(count++); /*分解素数的各位数字*/
if(number[count-1][2]%2!=0&& /*若可逆素数满足放在矩阵第一行*/
number[count-1][3]%2!=0&& /*和最后一行的条件,记录可逆素数的*/
number[count-1][2]!=5&& /*下标,计数器加1*/
number[count-1][3]!=5)
select[selecount++]=count-1;
}
}
larray[0][lcount[0]++]=number[0][0]/100; /*临时数组的第一行存前二位*/
larray[1][lcount[1]++]=number[0][0]/10; /*临时数组的第二行存前三位*/
for(i=1;i<count;i++) /*将素数不重复的前二、三位存入临时数组中*/
{
if(larray[0][lcount[0]-1]!=number[i][0]/100)
larray[0][lcount[0]++]=number[i][0]/100;
if(larray[1][lcount[1]-1]!=number[i][0]/10)
larray[1][lcount[1]++]=number[i][0]/10;
}
for(i1=0;i1<selecount;i1++) /*在第一行允许的汇聚围内穷举*/
{
array[0][0]=select[i1]; /*取对应的素数下标*/
copy_num(0); /*复制分解的素数*/
for(array[1][0]=0;array[1][0]<count;array[1][0]++) /*穷举第二行*/
{
copy_num(1); /*复制分解的数字*/
if(!comp_num(2))
continue; /*若每列的前两位的组成与素数相矛盾,则试探下一个数*/
for(array[2][0]=0;array[2][0]<count;array[2][0]++) /*穷举第三行*/
{
copy_num(2); /*复制分解的数字*/
if(!comp_num(3))
continue; /*若每列的前三位的组成与素数相矛盾,则试探下一个数*/
for(i4=0;i4<selecount;i4++) /*在最后一行允许的范围内穷举*/
{
array[3][0]=select[i4];
copy_num(3); /*复制分解的数字*/
for(flag=1,i=1;flag&&i<=4;i++) /*判断每列是否可逆素数*/
if(!find1(i))flag=0;
if(flag&&find2()) /*判断对角线是否为可逆素数*/
{ printf("No.%d\n",++cc); p_array(); } /*输出幻方矩阵*/
}
}
}
}
}
int num(int number) /*判断是否可逆素数*/
{
int j;
if(!ok(number)) return 0;
for(j=0;number>0;number/=10) /*将素数变为反序数*/
j=j*10+number%10;
if(!ok(j)) return 0; /*判断反序数是否为素数*/
return 1;
}
int ok(int number) /*判断是否为素数*/
{
int i,j;
if(number%2==0) return 0;
j=sqrt((double)number)+1;
for(i=3;i<=j;i+=2)
if(number%i==0) return 0;
return 1;
}
void process(int i) /*将第i个整数分解为数字并存入数组*/
{
int j,num;
num=number[i][0];
for(j=4;j>=1;j--,num/=10)
number[i][j]=num%10;
}
void copy_num(int i) /*将array[i][0]指向的素数的各位数字复制到array[i]中*/
{
int j;
for(j=1;j<=4;j++)
array[i][j]=number[array[i][0>[j];
}
int comp_num(int n) /*判断array中每列的前n位是否与可逆素数允许的前n位矛盾*/
{
static int ii; /*用内部静态变量保存前一次查找到的元素下标*/
static int jj; /*ii:前一次查找前二位的下标,jj:前一次查找前三位的下标*/
int i,num,k,*p; /*p:指向对应的要使用的前一次下标ii或jj*/
int *pcount; /*pcount:指向要使用的临时数组数量的计数器*/
switch(n){ /*根据n的值选择对应的一组控制变量*/
case 2:pcount=&lcount[0];p=ⅈbreak;
case 3:pcount=&lcount[1];p=&jj;break;
default:return 0;
}
for(i=1;i<=4;i++) /*对四列分别进行处理*/
{
for(num=0,k=0;k<n;k++) /*计算前n位数字代表的数值*/
num=num*10+array[k][i];
if(num<=larray[n-2][*p]) /*与前一次最后查找到的元素进行比较*/
for(;*p>=0&&num<larray[n-2][*p];(*p)--);/*若前次查找到的元素大,则向前找*/
else
for(;p<pcount&&num>larray[n-2][*p];(*p)++); /*否则向后找*/
if(*p<0||*p>=*pcount)
{
*p=0; return 0;
}
if(num!=larray[n-2][*p])
return 0; /*前n位不是可逆素数允许的值则返回0*/
}
return 1;
}
int find1(int i) /*判断列方向是否是可逆素数*/
{
int num,j;
for(num=0,j=0;j<4;j++)
num=num*10+array[j][i];
return find0(num);
}
int find2(void) /*判断对角线方向是否是可逆素数*/
{
int num1,num2,i,j;
for(num1=0,j=0;j<4;j++)
num1=num1*10+array[j][j+1];
for(num2=0,j=0,i=4;j<4;j++,i--)
num2=num2*10+array[j][i];
if(find0(num1)) return(find0(num2));
else return 0;
}
int find0(int num) /*查找是否为满足要求的可逆素数*/
{
static int j;
if(num<=number[j][0])for(;j>=0&&num<number[j][0];j--);
else for(;j<count&&num>number[j][0];j++);
if(j<0||j>=count){ j=0;return 0; }
if(num==number[j][0]) return 1;
else return 0;
}
void p_array(void) /*输出矩阵*/
{
int i,j;
for(i=0;i<4;i++)
{
for(j=1;j<=4;j++) printf("%d ",array[i][j]);
printf("\n");
}
}
*运行结果
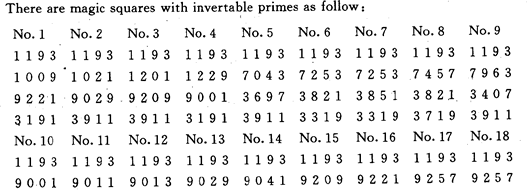
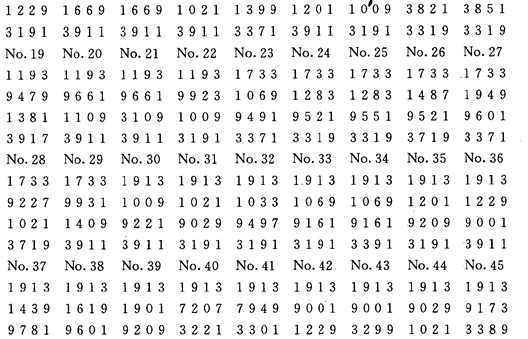




*问题的进一步讨论
程序中大量技巧是用于尽早发现矛盾,减少循环次数,缩短运行时间。从实际效果看是相当不错的。但目前的程序仍然可以进一步优化。
当第四行设定了前三行后,尚未设定的行就没必要再使用穷举的方法,因为列方向设定好的三位数字已经限制了最后一个数字可能的取值,在可逆数中找出前三位数字与设定好的三位数字相同的素数。这些素数就是在这一列前面已设定好的三位数字的限制条件下可能的取值。此时每一列上只有不超过四个可能的取值。找出全部各列可能的取值(可能的四位可逆素数),求出它们的交集。若交集为空,即没有共同的可能取值,则列间数据相互矛盾否满足则将交集中的数据填 入矩阵中就是题目的一个解。
算法可再进一步优化。先穷举一、二和四列的数据,然后用上面的算法来确定第三行的值,这样可进一步缩小穷举的范围,提高运行效率。
分析输出的结果。可以看出本题的基本解只有17种,每个解可通过旋转与反射获得同构的其它7个解,可以进一步改进程序,只输出17个基本解。
*思考题
用1到16构成一个四阶幻方,要求任意相邻两个方格中的数字之和均为素数。
 打印本文
打印本文  关闭窗口
关闭窗口